This column is the first in a 4-part series from Dr. Taeho Jo titled "AI in Medicine: From Nobel Discoveries to Clinical Frontiers". 

Imagine a piece of white paper. Let's draw two black dots and two white dots on it, alternating like this.

(Figure 1. Two black dots and two white dots arranged in an X pattern.)

Consider this puzzle: How can you fold this paper just once so that the black dots and white dots are separated without ending up in the same space? For example, if you fold it vertically down the middle, as shown in Figure2, the left side gets one black dot, and one white dot mixed together. The right side also gets one black dot and one white dot.

(Figure 2. Folding the paper vertically down the middle)

If you fold it diagonally, both black and white dots can end up in the same space. Another fold might also mix the colors. Figure 3 shows other possible folds that also mix the colors.

(Figure 3. Various folding attempts that all fail to separate the dots by color)

This simple puzzle might be more significant than it appears. Its underlying principle connects to the very foundations of AI—foundations upon which work was built that, decades later, led to Nobel Prizes for these five people shown in Figure 4.

(Figure 4. Recipients of the 2024 Nobel Prizes for AI Research)

The 2024 Nobel Prizes were truly special. Dr. John Hopfield and Dr. Geoffrey Hinton, who laid the foundations of AI and deep learning, received the Physics prize. Dr. Demis Hassabis and Dr. John Jumper, who successfully applied this technology to protein structure prediction, won the Chemistry prize. It felt like a year where AI swept the Nobel Prizes.

Over this four-column series, we look closely at what this Nobel-winning AI technology is, how it developed, and what it may bring in the future. This exploration can help identify what preparations are needed as AI rapidly advances.

The Essence of AI

First, let’s explore the essence of AI, its development process, and the core achievements contributed by Dr. Hopfield and Dr. Hinton. Let's return to the paper puzzle presented earlier.

The problem was: Can you take the black and white dots arranged in an alternating X shape and, with just one fold, ensure that dots of the same color don't end up in the same space?

To put it simply, this is impossible under the given conditions. But that doesn't mean there's no solution. Consider certain matchstick puzzles, like making four equilateral triangles using only six matchsticks. You can't solve this using ordinary flat methods either, as shown in Figure 5.

 (Figure 5. A puzzle to create four equilateral triangles using six matchsticks)

However, if you build a pyramid shape, the problem is solved. Moving beyond the 2D plane and thinking in 3D makes much more possible, as illustrated in Figure 6. 

 (Figure 6. 3D solution to the matchstick puzzle)

The paper puzzle is similar. It couldn't be solved by approaching it in 2D.

But by folding it in 3D, like shown in Figure 7: 

 (Figure 7: 3D solution to the dot separation puzzle)

You can fold two parts simultaneously and separate the colors without overlapping them in the same space. So, increasing the dimension to perform two tasks at once – that was the key to solving the problem.

Actually, the basic principle of AI is quite simple: drawing a proper 'line' or boundary. For example, consider distributions of healthy individuals and Alzheimer's disease (AD) patients. A medical AI using this data ultimately performs the task of drawing a line separating these two groups, as shown in Figure 8.

 (Figure 8. Boundary line between healthy individuals and AD patients)

This way, when a new sample is added, it can predict whether the sample is healthy or indicates AD. The paper puzzle represents a case where drawing a simple boundary line is tricky, as illustrated in Figure 9. 

 (Figure 9. Visual representation of the XOR problem.)

It refers to exactly this kind of situation, known as the XOR problem. Early AI absolutely had to solve this foundational problem   before it could progress to more complex tasks. Indeed, the effort to address such challenges led to the development of the Perceptron in 1957, the most basic tool for drawing lines at the time, shown in Figure 10: 

 (Figure 10. Basic structure and operation principle of the Perceptron)

However, it couldn't do more than draw a simple line. To solve the XOR problem, data scientists upgraded the Perceptron as shown in Figure 11:  

 (Figure 11. Solving the XOR problem using a multi-layer perceptron)

They added an invisible layer in the middle. This method, analogous to solving the paper puzzle by folding, created a new layer allowing two calculations to happen simultaneously, as depicted in Figure 12. 

 (Figure 12. Visualization of how a multi-layer perceptron works.)

This approach is called a 'Multi-Layer Perceptron' (MLP). However, this wasn't a complete solution either. Because the hidden layer was literally hidden, its contents couldn't be seen. Being unable to see the middle contents also meant being unable to see and adjust the weights within it. Research on how to train these hidden weights continued for decades. The biggest advance was a method called 'backpropagation', illustrated in Figure 13. 

 (Figure 13. Basic principle of the backpropagation algorithm)

As the diagram illustrates, the process begins by calculating the error at the output layer through a comparison of the prediction and the actual value. Subsequently, this error is propagated backward, with the weights of each hidden layer being adjusted sequentially. Nevertheless, this approach also presented certain limitations.  

  (Figure 14. Signal transmission problem in the backpropagation process.)

The further back the error signal goes (closer to the input layer), the influence of the error gradually fades and almost disappears. It's like a whispered message getting fainter as it passes down a line, becoming almost inaudible at the front. This is called the 'vanishing gradient' problem, and solving it took another  extended period. Eventually, various mathematical tools were developed to ensure the signal propagated effectively, gradually resolving the issue , as shown in Figure 15. 

 (Figure 15. Various activation functions and their characteristics.)

Nobel Prize-Winning Contributions

This progress did not happen overnight, nor was it the effort of just one or two people. Among the numerous contributors, Dr. John Hopfield and Dr. Geoffrey Hinton, who received the Nobel Prize in 2024, are arguably the scholars who provided the most crucial insights for solving these problems.

First, Dr. Hopfield researched how information is stored, and memories are recalled. He wanted to enable computers to recall complete memories from incomplete information, just like our brains do. So, he developed a system called the 'Hopfield Network,' where multiple nodes are interconnected, as shown in Figure 16.

 (Figure 16. Structure of a Hopfield Network. (Source: Wikipedia))

Each node influences and is influenced by others, storing, and retrieving information. Because all nodes are bidirectionally connected, the entire pattern can be restored even if some information is lost. However, the Hopfield Network had limitations. It didn't work well if too many patterns were stored, and it couldn't generate new patterns.

So, Dr. Hinton improved upon this by creating the Boltzmann Machine. The key feature of the Boltzmann Machine was the addition of hidden nodes, as shown in Figure 17.

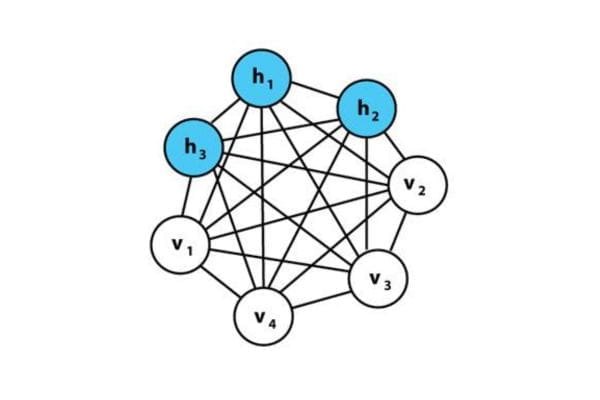 (Figure 17. Structure of a Boltzmann Machine. (Source: Wikipedia))

Like adding a hidden layer earlier, the addition of these hidden nodes (marked in blue, h) allowed for more effective learning of complex patterns. It used a principle similar to how we remember things not just by their visible features but also by invisible characteristics stored alongside them. 

Dr. Hinton later developed the Boltzmann Machine further into the RBM (Restricted Boltzmann Machine). As Figure 18 indicates, there are connections only between the visible and hidden layers; nodes within the same layer are not connected. By restricting connections like this, learning became more efficient. Stacking these RBMs layer upon layer resulted in the DBN (Deep Belief Network), where each layer sequentially learns higher-level features.

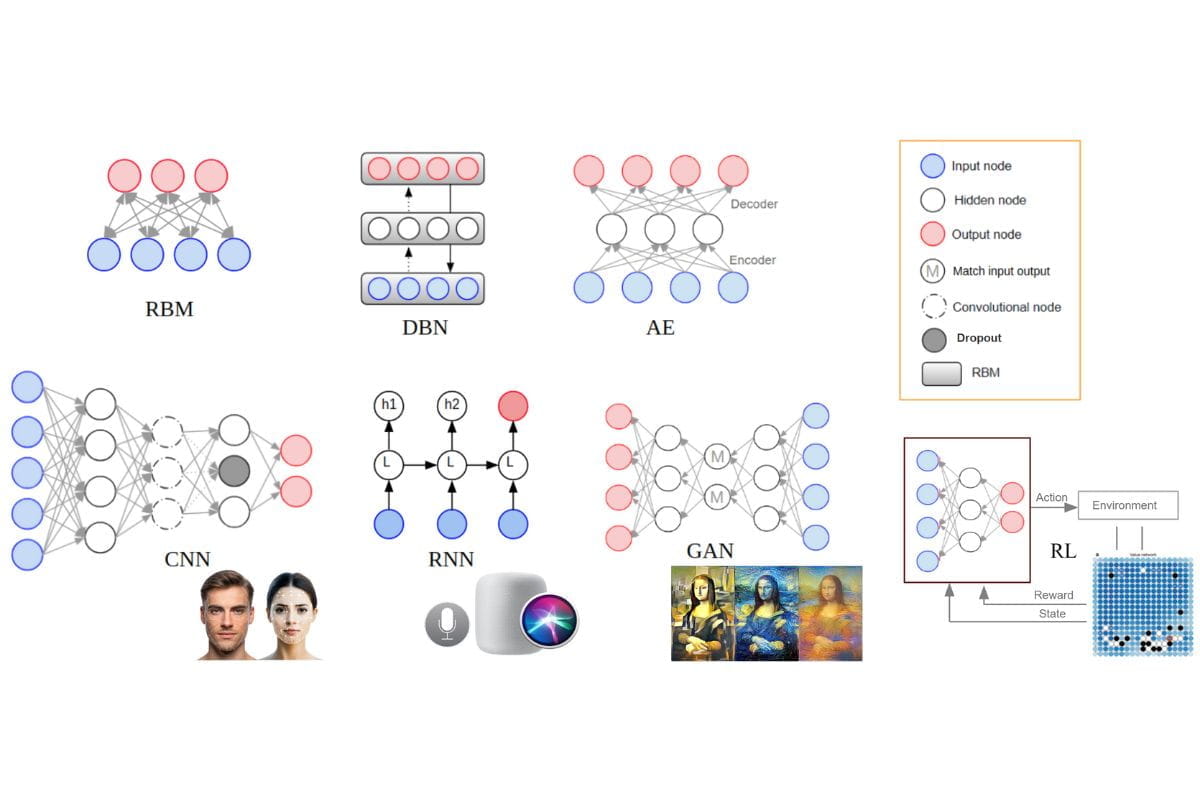
 (Figure 18. Restricted Boltzmann Machine and the evolution of modern AI technologies.)

This idea was developed into various forms by Dr. Hinton's team and other scientists. First, the Autoencoder (AE) allowed learning core data features by compressing data into fewer dimensions and then reconstructing it. CNN (Convolutional Neural Network) is based on the idea of extracting important image features step-by-step; it's used for recognizing things in photos, like Face ID, or understanding road conditions for self-driving cars. 

RNN (Recurrent Neural Network) processes sequential data by remembering previous information. RNNs use past information to predict the next step, becoming the foundation for modern language models and later evolving into models like Transformers, which led to the current LLM, such as ChatGPT. GAN (Generative Adversarial Network) uses the idea of two neural networks competing and improving each other; it has developed into technology that creates images hard to distinguish from real ones or the generative images seen today. 

Finally, Reinforcement Learning (RL) solves problems by finding the best choice in a given situation through trial and error; it addresses strategic decision-making problems like those solved by AlphaGo. 

Essentially, the diagram illustrates concepts that encompass almost the entirety of today's AI innovation. Dr. Hinton, being central to this research, received the Nobel Prize for his contributions that led the current AI and deep learning revolution. 

Conclusion

To summarize: Various experiments, like the backpropagation algorithm, were conducted to solve the XOR problem and the hidden layer learning problem. Decades of continuous effort built upon these experiments, leading to today's AI technology development. The fundamental principles presented by Dr. John Hopfield and Dr. Geoffrey Hinton during this process became the foundation of modern AI technology, which is the decisive reason they received the Nobel Prize. 

It's noteworthy that among the AI developers who inherited and advanced their research, other Nobel laureates emerged. The field where they applied AI is protein structure prediction. Why this is an important problem, and what solutions deep learning offered, will be explored in the next column. 

References

1. Jo, T. (2025).Deep Learning for Everyone(4th Revised Edition). Gilbut Publishing.Figures 1-3, 5-15, and 18.
2. Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities.Proceedings of the National Academy of Sciences, 79(8), 2554-2558.
3. Hinton, G. E., & Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks.Science, 313(5786), 504-507.
4. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors.Nature, 323(6088), 533-536.
5. Hinton, G. E., Osindero, S., & Teh, Y. W. (2006). A fast learning algorithm for deep belief nets.Neural Computation, 18(7), 1527-1554.
6. Wikipedia.Hopfield Network.Figure 16.
7. Wikipedia.Boltzmann Machine.Figure 17.
8. The Nobel Foundation. (2024).The Nobel Prize in Physics 2024.Figure 4.